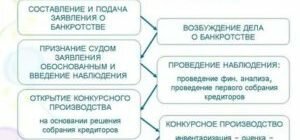
Этапы торгов в конкурсном производстве Действия организатора торгов (включая конкурсного управляющего) в отношении имущества
Расчет процентов по правилам статьи 395 ГК РФ Постоянная ссылка на расчет: http://395gk.ru Информация,
Почему кредитная история плохая Негативная информация о заемщике может стать причиной отказа в кредитах
Порядок проведения торгов при банкротстве Имущество должника продается на торгах, которые, как правило,
Федеральный закон «О несостоятельности (банкротстве)» (127-ФЗ) 2021, 2020 Юридическая грамотность населения выросла, и банкротство
Загадки про одежду | — Сказочник №13 Загадки про одежду с ответами для детей
Банкротство – что это Термин «банкротство» произошел от итальянского banca rotta («сломанная скамья»). В
Какое предприятие можно считать банкротом Формальные признаки банкротства представлены в Законе РФ «О несостоятельности».
Завершённые судебные дела Определение термина «банкротство» Банкротство, или неплатежеспособность (англ. » bankruptcy») – это
Какое предприятие можно считать банкротом Формальные признаки банкротства представлены в Законе РФ «О несостоятельности».
Банкротство муниципального предприятия Данный тип предприятий управляется единоличным руководителем, который устанавливается собственником. Все вопросы
Может ли банк списать долг по автокредиту? Заёмщики, которые столкнулись с большими финансовыми проблемами,
Кому может понадобиться информация из списка Изначально необходимо обращать внимание на то, что в
Что такое исполнительное производство при банкротстве? Исполнительное производство – это специальная процедура по принудительному
Регулировка деятельности страховых компаний В последнее время отмечается тенденция участившегося сокращения страховых организаций на
Кто может подать иск о несостоятельности юрлица? В соответствии со ст. 224 АПК РФ
За чей счет банкротство? Как правило, банкротство — процедура долгая. Результаты — не всегда
Оспаривание сделок физического лица при банкротстве Подозрительные сделки2. Сделки с предпочтениемОсобенности оспаривания сделок в
Может ли пенсионер объявить себя банкротом? Государство не предусмотрело каких-либо особых правил для банкротства
Кого интересует информация? Информация о банкротстве нужна потенциальным партнерам и многотысячному штабу сотрудников обанкроченной